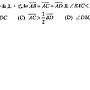Re: [中學] 國中競試題

: 請教此題
: 答案為 128205
: 只想到後面是05 前面不知怎麼思考
: 感謝你們。
假設n = \sum_{i=1:n} [a_i * 10^(i-1)]
已知 a_1 = 5,令a_0 = 0
m = 5 * 10^(n-1) + \sum_{i=2:n} [a_i * 10^(i-2)]
所以 5 = 4 * a_n + c_n, c_n 為進位到第n為的數。
又因為 1 <= a_n <= 9 所以 a_n = 1, c_n = 1.
同時 4 a_1 = 20 = 0 = a_2 (mod 10)
所以 n = 1____05 => 1___205 => 1__8205 => 128205
4n=m = 51____0 => 51___20 => 51__820 => 512820
最後一步要稍微推論一下,大概就是
(10 + a_{n-1}) * 4 + c_{n-1} = 51
c_{n-1} = a_{n-2} * 4 + c_{n-2} (mod 10)
a_{n-1} = a_{n-2} * 4 + c_{n-3} (mod 10)
然後因為a_n-2=8,c_{n-3}=0,所以a_{n-1}=2剛好是解
所以最小n就是 128205
所以c_n-1=3
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 140.109.23.210
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1443766937.A.740.html
討論串 (同標題文章)